Algorithms

Representing an area

The obstacles supposed to be present in the arena have a minimum size of 5cm*5cm. The maximum size of the arena is 4m*4m. For the simulation, the arena will be represented by a set of cells of dimension 5cm*5cm. We randomly generate blocks in the map representing walls. The density of obstacles is set with a probability p of presence of obstacles.
In the example below, the y-axis is inverted and the robot is supposed to begin from the top of the arena.

Map = np.array([[0 for i in range(w)] for j in range(h)]) # code : 0 = nothing ; 1 = wall

def rectangle(w1,h1,w2,h2):
    """
    Colorate the rectangle from (h1,w1) to (h2,w2) as a wall.
    """
    Map[h1:h2,w1:w2] = 1
	
def build_map_blocs_wall():
    """
    Building a whole map with:
    - probability p to get the place of obstacles
    - random size of rectangular obstacle
    """
    # Editing the border
    Map[:,0] = 1
    Map[-1,:] = 1
    Map[:,-1] = 1

    # Choosing some filled pixel randomly with a probability p
    for i in range(9,h-5):
        for j in range(5,w-5):
            if Map[i][j] !=1:
                Map[i][j] = np.random.binomial(1,p)
                if Map[i][j] ==1:
                    rectangle(j,i,j+random.randint(1,10),i+random.randint(1,10))
			

Representing the robot

Our robot is situated inside a 22.5cm diameter circle and we have to represent it in a grid of 5cm*5cm cells. The secure mode is preferable, meaning that it will be more useful to get the obstacles in a range of 25cm in front of the robot than in a range of 20cm. In the algorithm, we assume that thanks to the "circular shape" of the robot, the rotation can take place without any issues and without any checks.
Considering these elements, the robot will take 5 cells in width and 5 cells in height.

The robot is represented by a position (describing the center of the robot) (globx,globy) (boxes in the map) or (globX,globY), global position in centimeters in the map. The global angle of the robot is TETA. The angle TETA is linked with two variables (dirX or directionX and dirY (local) or directionY (global)) making easy to manipulate global positionning variable.

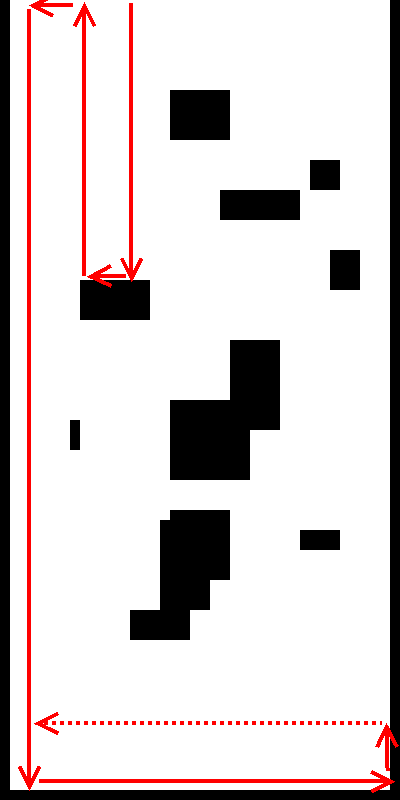
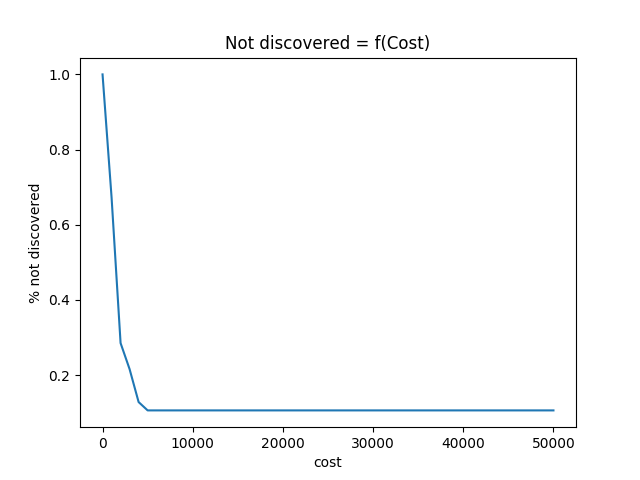
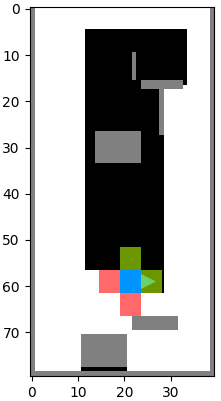
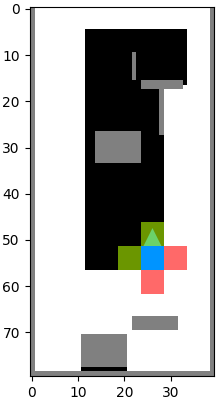
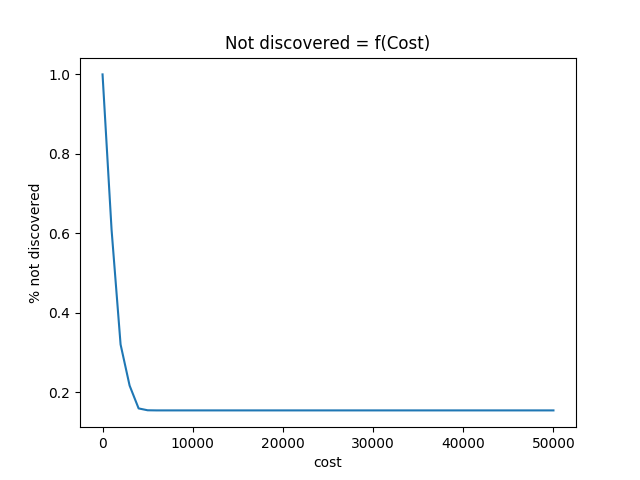
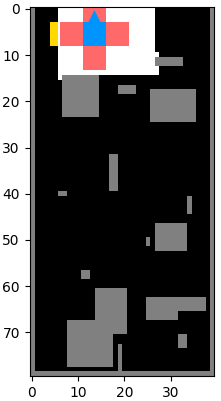
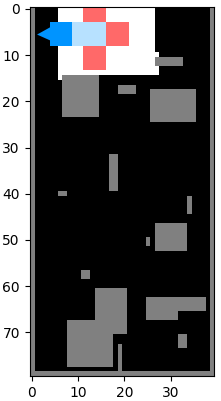
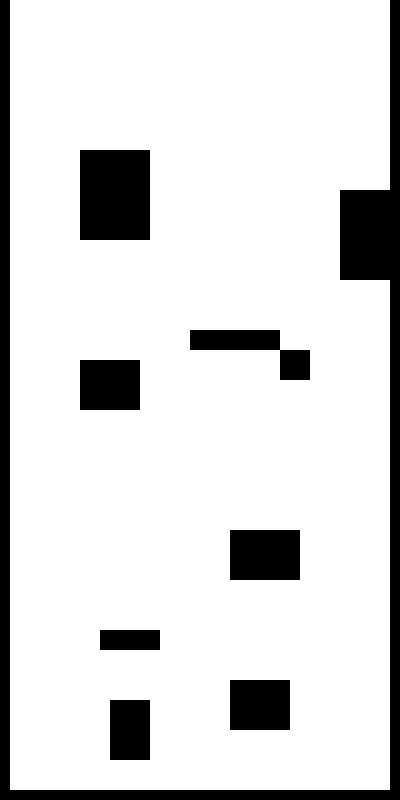Implementing basic functions of the robot

To reduce the difficulty of designing the algorithm, we limit our functions to "move forward", "rotation to either 90, 180 or 270 degrees" and "test if the robot can move forward"

Test if movement forward is possible :

def can_move_forward():
    """
    Discover the cells situated just in front of the robot and returns a boolean : True if the robot can move forward..
    """
    global globx
    global globX
    global globy
    global globY
    global TETA
    global directionX
    global directionY
    global cost
    global Map2
    is_possible=True

    # Check if the robot won't go outside the arena
    if (directionY==1 and globy==h-2) or (directionY==-1 and globy==2) or (directionX==1 and globx==w-2) or (directionX==-1 and globx==2) :
        is_possible = False

    # The 5 following statements enable to test the 5 cells situated in front of the robot
    if Map[globy+3*directionY-2*null(directionY),globx+3*directionX-2*null(directionX)]==1:
        is_possible = False 
        Map2[globy+3*directionY-2*null(directionY),globx+3*directionX-2*null(directionX)]=128
    else:
        Map2[globy+3*directionY-2*null(directionY),globx+3*directionX-2*null(directionX)]=255
        
    if Map[globy+3*directionY-null(directionY),globx+3*directionX-null(directionX)]==1:
        is_possible = False 
        Map2[globy+3*directionY-null(directionY),globx+3*directionX-null(directionX)]=128
    else:
        Map2[globy+3*directionY-null(directionY),globx+3*directionX-null(directionX)]=255

    if Map[globy+3*directionY,globx+3*directionX]==1:
        is_possible = False
        Map2[globy+3*directionY,globx+3*directionX]=128
    else:
        Map2[globy+3*directionY,globx+3*directionX]=255

    if Map[globy+3*directionY+null(directionY),globx+3*directionX+null(directionX)]==1:
        is_possible = False
        Map2[globy+3*directionY+null(directionY),globx+3*directionX+null(directionX)]=128
    else:
        Map2[globy+3*directionY+null(directionY),globx+3*directionX+null(directionX)]=255

    if Map[globy+3*directionY+2*null(directionY),globx+3*directionX+2*null(directionX)]==1:
        is_possible = False
        Map2[globy+3*directionY+2*null(directionY),globx+3*directionX+2*null(directionX)]=128
    else:
        Map2[globy+3*directionY+2*null(directionY),globx+3*directionX+2*null(directionX)]=255

    # assess the cost represented by the use of the function
    increase_cost(2)
    
    return is_possible
			

Move forward and rotate :

def move_forward():
    """
    The function enables to move the robot 5cm forward if it is possible.
    It returns True if the movement has been possible.
    """
    global globx
    global globX
    global globy
    global globY
    global TETA
    global directionX
    global directionY
    global cost
    if can_move_forward():
        globX=globX+5*directionX
        globY=globY+5*directionY
        globx=int(globX/5)
        globy=int(globY/5)
        increase_cost(1)
        return True
    else:
        return False

def move_forward_until(max_pos):
    """
    The function enables to move the robot forward until max_pos has been reached or the robot cannot move anymore.
    It returns the number of cells the robot has been able to do.
    """
    global globx
    global globX
    global globy
    global globY
    global TETA
    global directionX
    global directionY
    global cost
    i = 0
    while i < max_pos and can_move_forward():
        globX=globX+5*directionX
        globY=globY+5*directionY
        globx=int(globX/5)
        globy=int(globY/5)
        increase_cost(1)
        i=i+1
    return i

def rotate(angle):
    """
    The function enables to rotate the robot of a certain angle.
    """
    global TETA
    global directionX
    global directionY
    global cost
    TETA=(TETA+angle)%360
    if TETA==0:
        directionX = 0
        directionY = 1
    elif TETA==90:
        directionX = 1
        directionY = 0
    elif TETA ==180:
        directionX=0
        directionY=-1
    else:
        directionX=-1
        directionY=0
    increase_cost(1)
			

Assess the efficiency of an algorithm

To assess the efficiency of our algorithms, we have to take into account 2 parameters : a variable cost, representing the cost in time (estimation) for each action and the pourcentage of cell that are still not discovered. The metric used for the cost is the following one :

First basic Algorithm

The first algorithm we tested is a simple one. Here is the principle :

"Caterpillar" algorithm

# CATERPILLAR ALGORITHM #

def algo_chenille(i):
    global cost
    global threshold
    global costList
    global undiscoveredList
    while cost <= threshold:
        terminated = False
        arg = 0
        while not terminated:
            move_forward_until(max([h,w]))
            rotate(90)
            nb = move_forward_until(5)
            if nb == 0:
                arg = arg+1
            rotate(90)
            move_forward_until(max([h,w]))
            rotate(-90)
            nb = move_forward_until(5)
            if nb == 0:
                arg = arg+1
            rotate(-90)
            if arg==2:
                terminated = True
            arg = 0
        rotate(-90)
			

Performance for this algorithm

Our Algorithm

Theory

Simple Exploration Algorithm

This time we use a little knowledge of the map. The robot will prefer to go left or right if the area in front of it is unreachable or already disclosed.

"Recursive" algorithm

# ASSESS IF A SPACE HAS BEEN DISCOVERED #
				
def disclosed(angle):
    """
    check if the cells linked to the direction corresponding to the angle have already been disclosed
    """
    global globx
    global globX
    global globy
    global globY
    global Map2
    angle = angle%360
    if angle==0:
        dirX = 0
        dirY = 1
    elif angle==90:
        dirX  = 1
        dirY = 0
    elif angle==180:
        dirX =0
        dirY=-1
    else:
        dirX =-1
        dirY=0
    # Determining if 1 of the 5 cells in front of the robot has not already been discovered.  
    if Map2[globy+3*dirY,globx+3*dirX]==0 or Map2[globy+3*dirY+null(dirY),globx+3*dirX+null(dirX)]==0 or Map2[globy+3*dirY+null(dirY),globx+3*dirX+2*null(dirX)]==0 or Map2[globy+3*dirY-null(dirY),globx+3*dirX-null(dirX)]==0 or Map2[globy+3*dirY-null(dirY),globx+3*dirX-2*null(dirX)]==0:
        return False
    else:
        return True				

# ALGORITHMS RECURSIVE #

def algo_recursive(i):
    global cost
    global threshold
    global costList
    global undiscoveredList
    while cost<=threshold:
        if not disclosed(TETA+0):
            move_forward()
        else:
            if not disclosed(TETA+90):
                rotate(90)
                move_forward()
            elif not disclosed(TETA-90):
                rotate(-90)
                move_forward()
            else:
                if can_move_forward():
                    move_forward()
                else:
                    if np.random.binomial(1,0.5)==1:
                            rotate(90)
                        else:
                            rotate(-90)
			

Performance for this algorithm

Our Algorithm

Theory

Advanced Exploration Algorithm

This time we use a little knowledge of the map. The robot will prefer to go left or right if the area in front of it is unreachable or already disclosed. To that extent, when the area in front of it is disclosed or unreachable, the robot analyzes his map, chooses the nearest position where the map has been undisclosed (without crossing obastcles) and go there.

"Recursive V2" algorithm

#################################################
    
# ADVANCED MOVING FUNCTIONS #

def nearest_undisclosed_free(angle):
    """
    The function returns the biggest number of 5cm-cell with the angle "angle" that the robot can do.
    """
    global globx
    global globX
    global globy
    global globY
    global Map2
    angle=angle%360
    if angle==0:
        dirX = 0
        dirY = 1
    elif angle==90:
        dirX  = 1
        dirY = 0
    elif angle==180:
        dirX =0
        dirY=-1
    else:
        dirX =-1
        dirY=0
        
    i=0
    case1=128
    case2=128
    case3=128
    case4=128
    case5=128
    
    # we check that the cells assessed are inisde the arena
    if globy+(3+i)*dirY+2*null(dirY)0 and globx+(3+i)*dirX+2*null(dirX)0:
        case1 = Map2[globy+(3+i)*dirY-2*null(dirY),globx+(3+i)*dirX-2*null(dirX)]
        case2 = Map2[globy+(3+i)*dirY-null(dirY),globx+(3+i)*dirX-null(dirX)]
        case3 = Map2[globy+(3+i)*dirY,globx+(3+i)*dirX]
        case4 = Map2[globy+(3+i)*dirY+null(dirY),globx+(3+i)*dirX+null(dirX)]
        case5 = Map2[globy+(3+i)*dirY+2*null(dirY),globx+(3+i)*dirX+2*null(dirX)]

    # we loop until a wall has been found and an undisclosed place has not been found
    while case1!=128 and case2!=128 and case3!=128 and case4!=128 and case5!=128 and globy+(3+i)*dirY+2*null(dirY)0 and globx+(3+i)*dirX+2*null(dirX)0:
        if case1!=0 and case2!=0 and case3!=0 and case4!=0 and case5!=0:
            i=i+1
            if globy+(3+i)*dirY+2*null(dirY)0 and globx+(3+i)*dirX+2*null(dirX)0:
                case1 = Map2[globy+(3+i)*dirY-2*null(dirY),globx+(3+i)*dirX-2*null(dirX)]
                case2 = Map2[globy+(3+i)*dirY-null(dirY),globx+(3+i)*dirX-null(dirX)]
                case3 = Map2[globy+(3+i)*dirY,globx+(3+i)*dirX]
                case4 = Map2[globy+(3+i)*dirY+null(dirY),globx+(3+i)*dirX+null(dirX)]
                case5 = Map2[globy+(3+i)*dirY+2*null(dirY),globx+(3+i)*dirX+2*null(dirX)]
        else:
            return i+1
    return 1000

def nearest_undisclosed_point():
    """return the angle the robot should take to go to the nearest undisclosed point in one of the four direction without obstacle between, 1000 if not exists"""
    global TETA
    global globx
    global globX
    global globy
    global globY
    angle=0
    minimum = nearest_undisclosed_free(TETA+angle)
    indexAngle = angle
    while angle < 270:
        angle=angle+90
        dist = nearest_undisclosed_free(TETA+angle)
        if dist < minimum:
            minimum=dist
            indexAngle=angle
    return indexAngle,minimum				

# ALGORITHMS RECURSIVE B #

def algo_recursive_b(i):
    global cost
    global threshold
    global costList
    global undiscoveredList
    while cost<=threshold:
        if not disclosed(TETA+0):
            move_forward()
        else:
            if not disclosed(TETA+90):
                rotate(90)
                move_forward()
            elif not disclosed(TETA-90):
                rotate(-90)
                move_forward()
            else:
                indexAngle,minimum = nearest_undisclosed_point()
                if minimum==1000:
                    if can_move_forward():
                        move_forward()
                    else:
                        if np.random.binomial(1,0.5)==1:
                            rotate(90)
                        else:
                            rotate(-90)
                else:
                    rotate(indexAngle)
                    move_forward_until(minimum)
			

Performance for this algorithm

Our Algorithm

Theory